Areas Between Curves: Thinking Outside the Vertical Box

- Calculus

When learning a number of new math concepts in a short period of time, it can be tempting to just remember the processes and apply them unconditionally, and it often works. However, by not trying to understand a problem first and going straight for the process, we can actually make our lives much more difficult than is necessary. Lets take a look at this by considering the problem of finding the area between $ x = y^2 - 4y $ and $ x = 2y-y^2 $. To this point in my calculus 1 course, we’ve generally found area’s via vertical rectangles. Having practiced problems enough times, the process for getting a solution gets familiar, routine. So lets take a look at the kind of work involved by just sticking with the routine.

A visual of the problem

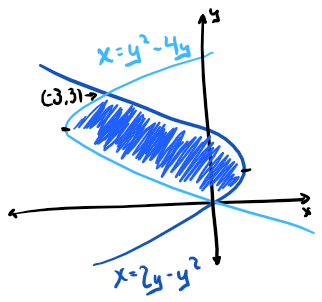
Sketch of the problem

Looking at this problem from the vertical rectangle perspective, we can see there’s a bit of a problem. A defining characteristic of the rectangle used in the Reimann sum that produces the area, is that each rectangle must have the same bounds, no matter where in the area space it is defined. However, in our current problem that’s not an option. In fact, on closer inspection, there are really 3 distinct types of rectangles that can be created here.

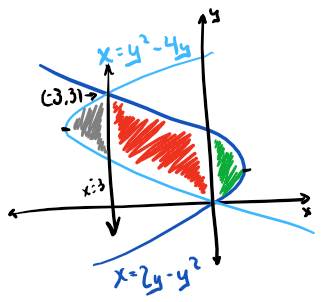
3 different regions

The strategy and prep work

The strategy is simple, we need to divide the area we are looking for into smaller regions for which we can find the area, then comine them. So, our general strategy is

\[ A = A_{r1} + A_{r2} + A_{r3}\]

Before we can begin, we must keep in mind that we are looking for vertical rectangles with a width of $ \Delta x $. That means the height must also be in terms of $ x $. Knowing this, lets get our two functions in terms of $ x $ before getting to the real work.

Function 1

\[\begin{aligned} x &= y^2 - 4y\\ x + 4 &= y^2 - 4y + 4\\ x+4& =(y-2)^2\\ \pm \sqrt{x+4}& =y-2\\ y& =2\pm \sqrt{x+4} \end{aligned}\]

Function 2

\[\begin{aligned} x& =2y-y^2\\ -x& =y^2-2y\\ 1-x& =y^2-2y+1\\ 1-x& =(y-1)^2\\ \pm \sqrt{1-x}& =y-1\\ y& =1\pm \sqrt{1-x} \end{aligned}\]

So really, there are actually 4 functions here:

\[\begin{aligned} y& =2+\sqrt{x+4} \ \ \text{<- top}\\ y& =2-\sqrt{x+4} \ \ \text{<- bottom}\\ y& =1+\sqrt{1-x} \ \ \text{<- top}\\ y& =1-\sqrt{1-x} \ \ \text{<- bottom} \end{aligned}\]

Each equation is split into the top half and the bottom half. This will be an important point to keep in mind later when determining the bounds for each region.

Region 1

We can see that the leftmost region only involves the curve $ x = y^2 - 4y $. The first step in finding the area of this region is to define its boundaries. In fact, we already have the first 3 defined for us if we inspect the graph.

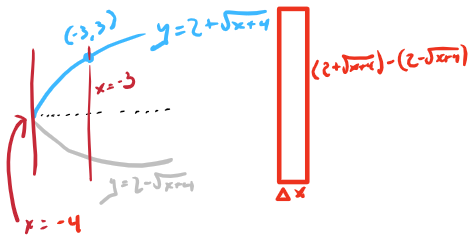
Region 1

The stickler, is that one on the left. If we think about it a moment though, the left boundary is really the minimum of the function $ x = y^2-4y $. We can find this by finding where $ x’=0 $ AND where its sign changes from negative to positive.

\[x'=2y-4\] \[\begin{aligned} x'& =0\\ 2y-4& =0\\ y& =2 \end{aligned}\]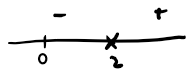

Region 1 number line

If we take a look at $ x’ $ on a number line, we can see that a min does occur at $ y = 2 $. Therefore,

\[\begin{aligned} x& =(2)^2-4(2) = -4 \end{aligned}\]

is the left boundary for this region.

\[\begin{aligned} A_{r1}& =\int_{-4}^{-3}[(2+\sqrt{x+4})-(2-\sqrt{x+4})]\ dx\\ & =\int_{-4}^{-3}(2\sqrt{x+4})\ dx\\ & =2\int_{-4}^{-3}\sqrt{x+4}\ dx \end{aligned}\]

Hmm, well, I don’t really know how to take an integral of $ \sqrt{x+4} $, so let’s do some substitution.

\[\begin{aligned} \text{Let }u& = x + 4\\ \frac{du}{dx}&= 1\\ du& =\ dx. \end{aligned}\]

Then, the new points of integration are $ u(-4) = 0 $ and $ u(-3) = 1 $. Continuing on to solve for the area we have,

\[\begin{aligned} A_{r1}& =2\int_{0}^{1}\sqrt{u}\ du\\ & =2\int_{0}^{1}u^\frac{1}{2}\ du\\ & =2\left[\frac{2}{3}u^\frac{3}{2}\right]_{0}^{1}\\ & =2\left[\frac{2}{3}(1)^\frac{3}{2}-0\right]\\ & =2\left[\frac{2}{3}\right]\\ & =\frac{4}{3}\ \text{units}^2 \end{aligned}\]

There we go, the area of one region down.

Region 2

Region 2

This region isn’t so bad, we can see all of our boundaries pretty easily. So let’s get down to work.

\[\begin{aligned} A_{r2}& =\int_{-3}^{0}[(1+\sqrt{1-x})-(2-\sqrt{x+4})]\ dx\\ & =\int_{-3}^{0}(-1+\sqrt{1-x}+\sqrt{x+4})\ dx\\ \end{aligned}\]

Well, this looks fun. That $ -1 $ is no problem, but we’ve got two different radicals here, so substitution won’t work. At least, not a single substitution. Lets tackle the $ \sqrt{1+x} $ first.

\[\begin{aligned} \text{Let }u& = 1 - x \end{aligned}\] \[\begin{aligned} \frac{du}{dx}& = -1\\ -du& =dx \end{aligned}\]

The new points of integration are now $ u(-3) = 4 $ and $ u(0) = 1 $. When putting these points of integration back in, its extremely important to keep them in the proper order. It may be tempting to use 1 as the lower bound and 4 as the upper bound, but this would swap the order of the original x values of integration. This would provide the wrong answer, so, always make sure to retain the original order for these points of integration.

Now lets use $ v $ for the substitution of the second radical. In the case of $ \sqrt{x+4} $,

\[\begin{aligned} \text{Let }v& = x+4 \end{aligned}\] \[\begin{aligned} \frac{du}{dx}& = 1\\ du& =dx \end{aligned}\]

The new points of integration for this integral are now $ v(-3) = 1 $ and $ v(0) = 4 $. Filling all this into our $ A_{r2} $ equation, we have,

\[\begin{aligned} A_{r2}& =-\int_{-3}^{0}(1)\ dx - \int_{4}^{1}\sqrt{u}\ du + \int_{1}^{4}\sqrt{v}\ dv\\ & =-\left[x\right]_{-3}^{0} - \left[\frac{2}{3}u^\frac{3}{2}\right]_{4}^{1} + \left[\frac{2}{3}v^\frac{3}{2}\right]_{1}^{4}\\ & =-[0-(-3)]-\left[\frac{2}{3}(1)^\frac{3}{2}-\frac{2}{3}(4)^\frac{3}{2}\right] + \left[\frac{2}{3}(4)^\frac{3}{2}-\frac{2}{3}(1)^\frac{3}{2}\right]\\ & =-3-\left[\frac{2}{3}-\frac{16}{3}\right]+\left[\frac{16}{3}-\frac{2}{3}\right]\\ & =-3+\frac{14}{3}+\frac{14}{3}\\ & =-\frac{9}{3} + \frac{28}{3}\\ & =\frac{19}{3}\ \text{units}^2 \end{aligned}\]

Alright, that’s 2 regions down…

Region 3

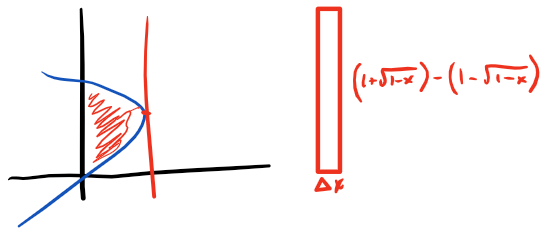
Region 3

This region is much like the first, only its bounded by the other curve. We can immediately define 3 of the boundaries for this region from the sketch.

For the right boundary, we can see that this occurs at the max of the curve $ x = 2y - y^2 $. This happens where $ x’ = 0 $ and its sign changes from positive to negative.

\[\begin{aligned} x'=2-2y\\ \end{aligned}\] \[\begin{aligned} x'& =0\\ 2-2y& =0\\ y& =1 \end{aligned}\]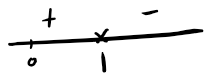

Region 3 number line

Looking at $ x’ $ on the number line, we can see there is a max at $ y = 1 $. Therefore,

\[\begin{aligned} x& =2(1)-(1)^2\\ & =1, \end{aligned}\]

is the right boundary for this region.

\[\begin{aligned} A_{r3}& =\int_{0}^{1}[(1+\sqrt{1-x})-(1-\sqrt{1-x})]\ dx\\ & =\int_{0}^{1}2\sqrt{1-x}\ dx\\ & =2\int_{0}^{1}\sqrt{1-x}\ dx \end{aligned}\]

Here’s another place we want to use substitution.

\[\begin{aligned} \text{Let }u& = 1 - x\\ \frac{du}{dx}&= -1\\ -du& =\ dx \end{aligned}\]

The new points of integration are $ u(0) = 1 $ and $ u(1) = 0 $. Here’s another place we need to be careful about maintaining the original order of the integration points, as the were in terms of $ x $.

\[\begin{aligned} A_{r3}& =-2\int_{1}^{0}\sqrt{u}\ du\\ & =-2\int_{1}^{0}u^\frac{1}{2}\ du\\ & =-2\left[\frac{2}{3}u^\frac{3}{2}\right]_{1}^{0}\\ & =-2\left[0-\frac{2}{3}{1}^\frac{3}{2}\right]\\ & =-2\left[-\frac{2}{3}\right]\\ & =\frac{4}{3}\ \text{units}^2 \end{aligned}\]

Putting it all together

Alright… well, that took a long time. What year is it now? Just kidding. Now that we have the 3 individual regions figured out, now comes the easy part, combining them all. Doing so, we arive at the final answer,

\[\begin{aligned} A& = A_{r1} + A_{r2} + A_{r3}\\ & =\frac{4}{3} + \frac{19}{3} + \frac{4}{3}\\ & =\frac{27}{3}\\ & =9\ \text{units}^2 \end{aligned}\]

The area between the two curves is $ 9\ \text{units}^2 $.

A simpler route

That all seemed like a lot of work, isn’t there a simpler way? There sure is and the clue lies in the fact that the equations were originally given in terms of $ y $. This makes it easy to set up the integral, lets look at the boundaries.

There we go, lets set this up and solve.

\[\begin{aligned} A& =\int_{0}^{3}[(2y-y^2)-(y^2-4y)]\ dy\\ & =\int_{0}^{3}(6y-2y^2)\ dy\\ & =\left[3y^2-\frac{2}{3}y^3\right]_{0}^{3}\\ & =[27 - 18]\\ & =9\ \text{units}^2 \end{aligned}\]

Ok, that was a less work, a lot less. So the moral of the story is to understand the problem and the tools at hand. Just looking at solving for the area between these two curves via vertical rectangles, its obvious there will be a lot of work involved, just from the setup. When this happens it doesn’t hurt to look outside the box, or in this case, literally looking at the problem from a different angle. It just might lead to a simpler solution and a lot of saved time.